Synkron detektering, principen bakom ”lock-in”-förstärkare, är en användbar teknik för att extrahera signaler som döljer sig väl under brusgolvet. Denna artikel diskuterar frekvensdomänoperationerna i synkron detektering, olika kretsimplementationer av tekniken samt för- och nackdelar med var och en av dem.

Synkron detektering är en användbar teknik för att extrahera lågnivåsignaler som döljer sig väl under brusgolvet och har många instrumentationstillämpningar. Några exempel inkluderar mätning av mycket litet motstånd, mätning av ljusabsorption eller -reflektion i närvaro av starkt bakgrundsljus, eller till och med töjningsmätning i närvaro av höga brusnivåer.
Många elektriska och fysiska system uppvisar ökat brus då frekvensen närmar sig likström. Till exempel har operationsförstärkare ett brus på 1/f och öppna ljusmätningssystem är föremål för brus från förändringar i omgivningsljuset på grund av solljus, glödlampor, lysrör, etc. Om du kan flytta mätningen bort från dessa lågfrekventa störningskällor kan du uppnå ett högre signal-brusförhållande och detektera mycket svagare signaler. Om du till exempel vill mäta mängden ljus som reflekteras från en yta kan ljuskällan moduleras några kilohertz, vilket gör det möjligt att mäta signaler som annars skulle begravas i lågfrekvent brus. Fig 1 visar hur modulering av signalen gör skillnaden mellan att vara under brusgolvet och en användbar mätning.
Det finns flera metoder för att modulera en givares excitationssignal. Den enklaste formen av modulering är att helt enkelt stänga av och slå på excitationssignalen upprepade gånger. Detta fungerar bra för att driva lysdioder och andra typer av excitation, som spänningen som går till en töjningsgivarbrygga, etc. Det fungerar särskilt bra då excitationskällan inte är lätt att modulera elektroniskt, som med glödlampor som används i många spektroskopiinstrument. I detta fall är moduleringen så enkel som att helt enkelt ”choppra” ljuset med en mekanisk skiva.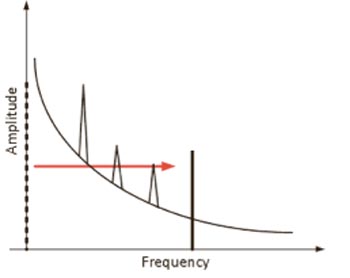

Fig 1. Modulering av signalen för att flytta den bort från bruskällor.

För att återskapa signalen i fig 1 kan du helt enkelt konstruera ett smalt bandpassfilter som tar bort alla frekvenser utom den som är av intresse. Därefter kan signalens amplitud mätas. I praktiken är det mycket utmanande att designa väldigt smala (högt Q) bandpassfilter med diskreta komponenter. Om specifikationen kräver ett extremt smalt filter kan det till och med vara omöjligt.
Ett alternativ är att använda synkron demodulering för att flytta den modulerade signalen tillbaka till likström, samtidigt som andra signaler som inte synkroniseras med referenssignalen filtreras bort. Ett instrument som använder denna teknik kallas lock-in-förstärkare.
Ett enkelt sätt att beskriva en lock-in-förstärkare är att börja med tillämpningen som visas i fig 2. En ljuskälla modulerad med 1 kHz belyser en provyta och en fotodiod mäter hur mycket ljus som reflekteras av ytan, vilket är proportionerligt till mängden föroreningar som har samlats. Anta att både referenssignalen och mätningen är sinusvågor (med samma frekvens och fas men olika amplitud). Anta att amplituden hos referenssignalen som driver fotodioden är konstant och att amplituden hos mätningen varierar med mängden ljus som reflekteras (i andra tillämpningar motsvarar detta den fysiska parameter som du mäter).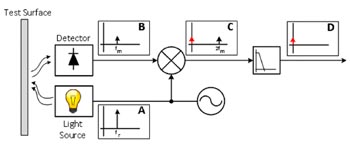

Fig 2. Mätning av ytkontaminering med en lock-in-förstärkare.

Resultatet av att multiplicera de två sinusvågorna är en signal med frekvenskomponenter med summa och skillnad av de två ingångssinusvågorna. I detta fall har de två sinusvågorna samma frekvens – Ekvation 1 visar hur resultatet är en signal vid likström och en annan vid dubbla den ursprungliga frekvensen (minustecknet indikerar att den har 180° fasförskjutning). Ett lågpassfilter avlägsnar sedan allt utom signalens likströmskomponent.

A sin(2πf_mt)· B sin(2πf_mt)
= ½AB – ½AB·cos(2π(f_m+f_m)·t)
= ½AB – ½AB cos(2π2f_mt)        [ekv 1]

Fördelen med att använda denna teknik blir mer uppenbar om du tänker dig en brusig insignal. Utsignalen från multiplikationssteget resulterar i att endast signalen vid modulationsfrekvensen flyttar tillbaka till likström och alla andra frekvenskomponenter flyttar till andra, icke-likströmsfrekvenser. Som exempel visar fig 3 ett system med starka bruskällor vid 50 Hz och 2,5 kHz samt en väldigt svag signal av intresse modulerad med en sinusvåg vid 1 kHz. Resultatet av att multiplicera insignalen med en referenssignal är en signal vid likström och andra signaler vid 950 Hz, 1,05 kHz, 1,5 kHz, 2 kHz och 3,5 kHz.  Likströmssignalen innehåller den önskade informationen, så du kan använda ett lågpassfilter för att avlägsna alla andra frekvenser.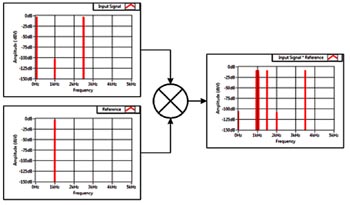

Fig 3. Synkron demodulering plockar ut en svag signal vid 1 kHz
i närvaro av starka bruskällor vid 50 Hz och 2,5 kHz.

Eventuella bruskomponenter som ligger nära den intressanta signalen kommer att uppträda vid frekvenser nära likström, så det är viktigt att välja en moduleringsfrekvens som inte har starka bruskällor i närheten. Om detta inte är möjligt kommer du behöva ett lågpassfilter med mycket låg gränsfrekvens och snabb svarstid, på bekostnad av lång inställningstid.

Praktiska tillämpningar
Att generera en sinusvåg för att modulera signalkällan kan vara opraktiskt och vissa system använder en fyrkantvåg istället. Det är mycket enklare att generera en fyrkantvåg som excitation än en sinusvåg eftersom det kan göras med något så enkelt som att låta utgången från en mikrokontroller växla en analog switch eller en MOSFET.
Kretsen i fig 4 är ett enkelt sätt att implementera en hårdvarubaserad lock-in-förstärkare. En mikrokontroller eller annan digital komponent genererar en fyrkantvåg som excitationssignal och denna får givaren att reagera. I fallet med fotodioden är den första förstärkaren en ström-till-spänningsomvandlare medan en töjningsgivarbrygga skulle kräva en instrumentförstärkare.
Samma signal som exciterar givaren styr SPDT-switchen ADG619. När excitationssignalen är positiv konfigurerar ADG619 förstärkaren för en förstärkning på +1, och när excitationen är negativ konfigurerar ADG619 förstärkaren för en förstärkning på -1 vilket praktiskt taget ”flippar” den negativa sidan av fyrkantvågen. Detta är matematiskt ekvivalent med multiplicering av den uppmätta signalen med referenssignalens fyrkantvåg. RC-filtret på utsignalen avlägsnar eventuella signaler på andra frekvenser och utspänningen är en likströmssignal som är lika med halva topp-till-topp-spänningen hos den uppmätta fyrkantvågen.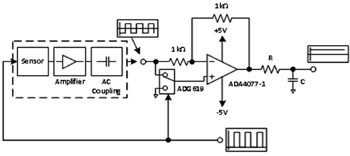

Fig 4. Lock-in-förstärkare med fyrkantvåg som excitation.

Även om kretsen är enkel är det viktigt att välja rätt operationsförstärkare för jobbet. AC-kopplingssteget för insignalen avlägsnar det mesta lågfrekventa bruset men varje brus på 1/f och förskjutningsfel från den sista förstärkaren i kedjan filtreras inte bort. ADA4077-1 har 250 nVpp brus från 0,1 Hz till 10 Hz och 0,55 µV/?C förskjutningsavdrift vilket gör den till en idealisk kandidat för denna tillämpning.
Användning av en fyrkantvågsbaserad lock-in-förstärkare kräver en enkel krets, men dess avstörningsprestanda är underlägsen ett system som använder sinusvågor. Figur 5 visar frekvensdomänrepresentationen av att använda en fyrkantvåg som givarexcitation samt referenssignalen. En fyrkantvåg består fundamentalt av en oändlig mängd av sinusvågor och alla udda övertoner. Multiplicering av två fyrkantvågor med samma frekvens innefattar att multiplicera varje sinuskomponent hos referenssignalen med varje sinuskomponent hos den uppmätta signalen. Resultatet är en likströmssignal som innehåller energin från varje överton i fyrkantvågen. Eventuella oönskade signaler som syns vid någon udda övertonsfrekvens kommer inte att filtreras bort (även om de kommer att skalas ned beroende på vilken överton de faller inom). Vid utformning av en fyrkantvågsbaserad lock-in-förstärkare är det viktigt att välja en moduleringsfrekvens vars övertoner inte ligger vid någon frekvens eller överton hos kända bruskällor. Till exempel, istället för att välja 1 kHz (vilken är den 20:e övertonen av 50 Hz) kan frekvensen 1,0375 kHz väljas som inte sammanfaller med övertoner hos 50 Hz eller 60 Hz.
Även med denna nackdel är kretsen enkel och billig. Att använda en lågbrusförstärkare och välja rätt modulationsfrekvens kan fortfarande resultera i en stor förbättring jämfört med att försöka göra en likströmsmätning.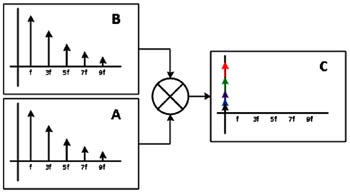

Fig 5. Om insignalen (A) och referenssignalen (B) båda är fyrkantvågor kan man genom att multiplicera ihop dem (C) effektivt demodulera varje överton hos insignalen.

Ett enkelt integrerat alternativ
Kretsen i fig 4 kräver en operationsförstärkare, en analog switch och några diskreta komponenter samt en referensklocka från en mikrokontroller. Ett alternativ till denna krets är att använda en integrerad synkron demodulator som ADA2200. Figur 6 visar de interna blocken i ADA2200 som inkluderar en buffrad ingång, ett programmerbart IIR-filter och en multiplikator. Den innehåller också ett block som förskjuter referenssignalen med 90° vilket gör det lätt att mäta eller kompensera för fasförskjutningar mellan referensklockan och insignalen. Fördelarna med denna operation förklaras i detalj i följande avsnitt.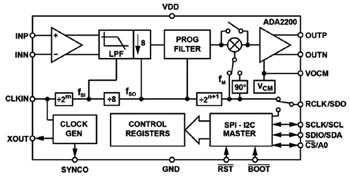

Fig 6. Intern arkitektur hos ADA2200.

Att implementera en lock-in-detekteringskrets med ADA2200 kräver helt enkelt att en klockfrekvens som är 64 gånger den önskade referensfrekvensen appliceras. Standardkonfigurationen för det programmerbara filtret är för bandpassrespons vilket eliminerar behovet av att växelströmskoppla signalen som för kretsen i fig 4. Den samplade analoga utgången på ADA2200 genererar bilder kring multiplar av samplingsfrekvensen. Du kan använda ett RC-filter följt av en sigma-delta-ADC för att ta bort dessa och endast mäta den demodulerade likströmskomponenten av signalen.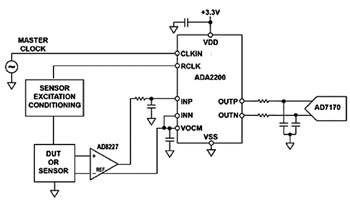

Fig 7. Lock-in-förstärkarimplementation med ADA2200.

Förbättring av fyrkantvågs-, lock-in-kretsen
Fig 8 visar en förbättring av en fyrkantvågsmodulerad krets. Om du exciterar givaren med en fyrkantvåg, men multiplicerar den uppmätta signalen med en sinusvåg som har samma frekvens och fas, så kommer bara signalens innehåll vid grundtonsfrekvensen flyttas till likström samtidigt som alla andra övertoner kommer flytta till icke-likströmsfrekvenser. Detta gör det enkelt att använda ett lågpassfilter och eliminera allt utom likströmskomponenten hos den uppmätta signalen.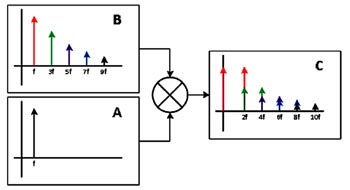

Fig 8. Användning av en sinusvåg som referenssignal förhindrar att brus demoduleras till likström.

Ytterligare en svårighet är att om det finns någon fasförskjutning mellan referenssignalen och den uppmätta signalen så kommer resultatet av att multiplicera de två resultera i en lägre amplitud på den resulterande utsignalen än om de var helt i fas. Detta kan inträffa om givarens signalbehandlingskrets inkluderar filter (som introducerar fasförskjutning). Med en analog lock-in-förstärkare är det enda sättet att adressera detta att inkludera ytterligare faskompensationskretsar i referenssignalvägen. Detta är inte trivialt eftersom kretsen behöver vara justerbar för att kompensera för olika fasförskjutningar, och den kommer att variera med temperatur, tolerans hos komponenter etc. Ett enklare alternativ är att lägga till ett andra multiplikatorsteg som multiplicerar den uppmätta signalen med en 90° fasförskjuten version av referensen. Resultatet av detta andra steg är en signal proportionerlig till ur-fas-komponenten av insignalen. Fig 9 visar detta koncept.
Utsignalerna från lågpassfiltren efter de två multipliceringsstegen är lågfrekventa signaler i proportion till i-fas (I) och kvadratur (Q) -komponenterna hos insignalen. För att beräkna storleken på insignalen tas helt enkelt summan av kvadraterna av I- och Q-utgångarna. En ytterligare fördel med denna arkitektur är att det också går att beräkna fasen mellan excitations-/referenssignalen och insignalen.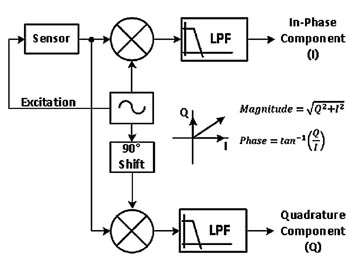

Fig 9. Användning av kvadraturversion av referenssignalen för att beräkna storlek och fas.

Alla system som hittills diskuterats genererar en referenssignal som exciterar en givare. En sista förfining av lock-in-förstärkaren är att tillåta en extern signal att agera referens. Som exempel visas i figur 10 ett system som använder bredbandigt glödlampsljus för att testa de optiska egenskaperna hos en yta. Ett system som detta kan mäta parametrar som till exempel reflektiviteten hos speglar eller mängden föroreningar på en yta. Det är mycket enklare att använda en mekanisk roterande huggskiva för att modulera en glödlampsljuskälla än att använda elektronisk modulering. En billig lägesgivare nära huggskivan genererar en fyrkantreferenssignal för att mata lock-in-förstärkaren. Snarare än att använda denna signal direkt genererar en faslåst loop en sinusvåg med samma frekvens och fas som den inmatade referensen. En nackdel med detta tillvägagångssätt är att den internt genererade sinusvågen måste ha låg distorsion.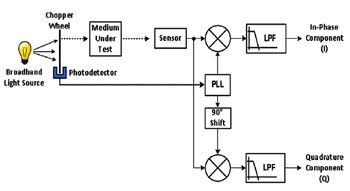

Fig 10. Användning av en PLL för att låsa på en extern referenssignal.

Även om detta system kan konstrueras med hjälp av diskreta PLLer och multiplikatorer så resulterar användning av en FPGA för att implementera lock-in-förstärkarens funktioner flera prestandafördelar. I Fig 11 visas en lock-in-förstärkare byggd med en FPGA och en front-end, baserad på den avdriftsfria förstärkaren ADA4528-1 och 24-bitars sigma-delta-omvandlaren AD7175.
En tillämpning som denna behöver inte mycket bandbredd så vi kan sätta lock-in-förstärkarens brusbandbredd på 50 Hz. Mätobjektet är igen en givare som kan exciteras externt. Förstärkaren ADA4528-1 är konfigurerad med en brusförstärkning på 20 för att dra nytta av hela omfånget hos signalomvandlaren (godtyckligt satt för detta exempel).
Även om likströmsfel inte påverkar mätningen är det fortfarande viktigt att minimera offsetdrift och 1/f-brus eftersom de kommer att minska det tillgängliga dynamiska omfånget, särskilt då förstärkaren är konfigurerad för hög förstärkning. ADA4528-1 har som mest 2,5 µV offsetfel vilket utgör endast 1 ppm av det fulla insignalsomfånget hos AD7175 (med en referens på 2,5 V).
Det digitala högpassfiltret efter signalomvandlaren avlägsnar all likströmsoffset och mycket lågfrekvent brus. För att beräkna det utgående bruset behöver vi veta spänningsbrustätheten hos AD7175. Databladet ger att signalomvandlarens brus är 5,9 µVrms med en utdatahastighet på 50 ksps då Sinc3+Sinc1-filter och insignalsbufferten används. Den ekvivalenta brusbandbredden med dessa inställningar är 21,7 kHz vilket resulterar I en spänningsbrustäthet på 40 nV/Hz. Det bredbandiga insignalsbruset för ADA4528 är 5,9 nV/Hz vilket syns på utsignalen som 118 nV/Hz och resulterar i en kombinerad brustäthet på 125 nV/Hz. Eftersom det digitala filtret har en ekvivalent brusbandbredd på bara 50 Hz är utsignalsbruset 881 nVrms. Med ett insignalsomfång på ±2,5 V resulterar detta I ett system med ett dynamiskt omfång på 126 dB. Vi kan byta bandbredd mot dynamiskt omfång genom att justera frekvenssvaret för lågpassfiltret. Till exempel, om vi sätter filtren för en ekvivalent brusbandbredd på 1 Hz får vi ett dynamiskt omfång på 143 dB, sätter vi bandbredden till 250 Hz får vi ett dynamiskt omfång på 119 dB.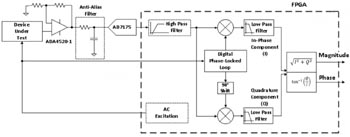

Fig 11. FPGA-baserad lock-in-förstärkare.

Den digitala faslåsta loopen genererar en sinusvåg låst till excitationssignalen (som kan vara en extern signal eller genereras internt i FPGA:n, den behöver inte heller vara en sinusvåg). Eventuella övertoner i referenssignalen kommer också att multipliceras med insignalen, vilket demodulerar brus och andra oönskade signaler som finns vid de harmoniserande frekvenserna, precis som då två fyrkantvågor multipliceras med varandra (som i fig 5). En fördel med att generera denna referenssinusvåg digitalt är att det är relativt lätt att generera en signal med mycket låg distorsion bara genom att justera talprecisionen. I fig 12 visas som exempel fyra digitalt genererade sinusvågor med 4, 8, 16 och 32 bitars precision. Det är uppenbart att 4 bitars precision ger en prestanda som liknar fallet i fig 5 men situationen förbättras snabbt genom att använda högre precision. Vid 16 bitars precision skulle det krävas en hel del arbete att generera en analog signal med så pass låg total harmonisk distorsion (THD), och vid 32 bitar där THD är över -200 dB skulle det vara omöjligt att åstadkomma med en analog krets. Dessutom är dessa signaler helt repeterbara eftersom de är digitalt genererade. När signalen väl har konverterats till digital information och kommer in till FPGAn finns inget ytterligare brus eller någon förskjutning att ta hänsyn till.
Efter multiplikatorerna tar lågpassfiltren bort eventuella högfrekvenskomponenter och skickar ut i-fas- och kvadraturkomponenterna av signalen. Om vi fortsätter anta att den ekvivalenta brusbandbredden hos filtren endast är 50 Hz finns det ingen anledning att leverera data med den ursprungliga samplingshastigheten på 250 ksps. Lågpassfiltret kan inkludera ett decimeringssteg för att reducera den utgående datahastigheten. Det sista steget i processen är att beräkna storleken och fasen hos insignalen utifrån i-fas- och kvadraturkomponenterna.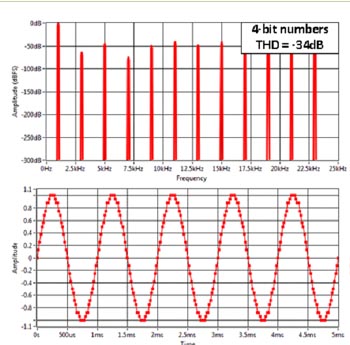




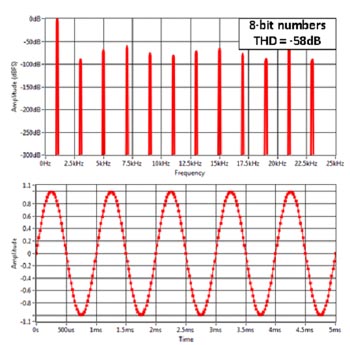
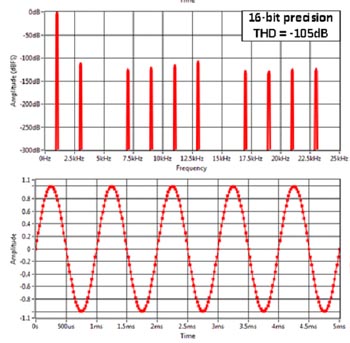
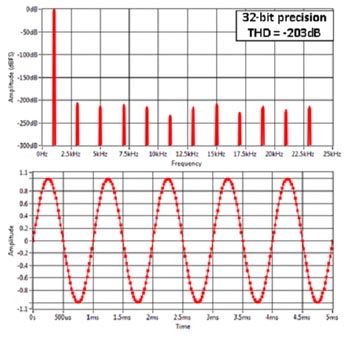
Fig 12. Numeriskt genererade sinusvågor med olika talprecision.

Lock-in med hög precision
Små, lågfrekventa signaler begravda i brusgolvet kan vara svåra att mäta, men genom att tillämpa modulering och lock-in-förstärkarteknik kan mätningar med hög precision uppnås. I sin enklaste form kan en lock-in-förstärkare vara en operationsförstärkare som växlar mellan två förstärkningar. Även om detta inte ger den lägsta brusprestandan gör enkelheten och den låga kostnaden detta till ett mycket attraktivt alternativ till en enkel likströmsmätning. En förbättring utifrån denna krets är att använda en sinusformad referenssignal och en multiplikator, men detta kan vara svårt att genomföra i den analoga domänen. För bästa prestanda bör en lågbrusig, högupplöst sigma-delta-omvandlare som AD7175 övervägas för att digitalisera insignalen, och sedan generera den sinusformade referenssignalen och alla de andra delarna i lock-in-förstärkaren i den digitala domänen.

Om författaren
Luis Orozco [luis.orozco@analog.com] är systemtillämpningsingenjör inom Industry and Instrumentation hos ADI. Han fokuserar på precisionsinstrumentering, kemisk analys och miljöövervakningstillämpningar. Luis började på ADI i februari 2011. Innan han kom till ADI designade han datainsamlingsutrustning i över tio år.

Filed under: Analogteknik