I arbetet med avlusning och validering av både digitala och RF-konstruktioner kan FFT (Fast Fourier Transform) och andra matematiska operationer göra oscilloskopet till ett värdefullt instrument då konstruktören tar konstruktionen från prototypstadiet till produktion.

Vid exempelvis digitala konstruktioner kan FFT-funktionen i ett oscilloskop snabbt markera innehållet i signaler som överförs via strömförsörjningsskenor och ge kunskaper som kan peka ut störningskällan. Det är viktigt eftersom sådana signaler kan överföras för att ge störningar i andra delar av konstruktionen, minska marginalerna och potentiellt hindra utvecklingen bortom prototypstadiet tills problemet är åtgärdat.
Ett FFT-spektrum är också till hjälp när man undersöker mer komplexa signaler med ett brett spektrum för att kunna verifiera att rätt modulation sker. Med tidsgrindad FFT kan man ytterligare utvärdera en signals spektrala komponenter. Med matematiska funktioner för att se trender av frekvensändringar kan man snabbt kontrollera om ett klassisk modulationsschema är korrekt, som linjär frekvensmodulering av en ström av pulser. I den här artikeln  granskar vi några av dessa exempel och ser på hur mätningarna kan genomföras i praktiken.

FFT-mätning av inmatad sinusvåg
Ett oscilloskop med 1 GHz analog bandbredd och upp till en 5 GSa / s samplingshastighet användas för mätningarna. Det är två viktiga specifikationer som utmynnar i vilka slags mätningar som är möjliga.
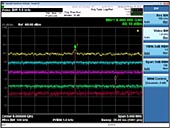
I ett första mätexempel fångar vi in en sinusvåg med 600 MHz, 632 mV (pp), 0 dBm, 1 mW sinussignal över 50 ohm (orange). Resultatet av FFT (vit) visas i fig 1.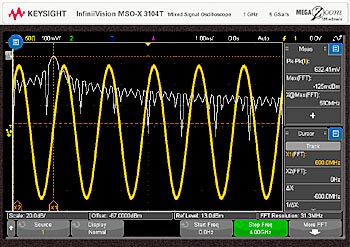

Fig 1. Tidsdomän capture vid 1 ns / div och FFT displayen från en 600 MHz sinusvåg ingång

Grunderna för FFT-mätningar
Det är viktigt att förstå hur oscilloskop samplingsegenskaper spelar in på kvaliteten hos denna FFT-mätning. Oscilloskopets analoga bandbredd, samplingshastighet, minnesdjup och tillhörande periodtid för signalinhämtning kan alla ha en djupgående inverkan på mätresultatet. Effekten påverkas starkt av testsignalens egenskaper och hur dessa signalegenskaper förhåller sig till oscilloskopets prestanda beträffande signalinsamling.
I vårt exempel mäter vi en enda 600 MHz sinusvågsignal och vill se signalens spektrala egenskaper i grunden. Oscilloskopet måste ha tillräckligt analog bandbredd för att inte dämpa signalens amplitud. Eftersom oscilloskop har maximalt 1 GHz analog bandbredd finns det gott om oscilloskop bandbredd för att mäta 600 MHz-signalen.
För att undvika vikning (aliasing) vid  digitaliseringsprocessen av signalen måste samplingen ske vid en hastighet som är åtminstone två gånger frekvensen för varje frekvens som finns i testsignalen. I denna enklaste exemplet med en 600 MHz sinusvåg skulle 1,2 GHz samplingsfrekvens behövas. Tydligt är 5 GSa/s hastighet  mer än tillräcklig. Senare i texten skall vi dock visa att vid viss inställning av  tid/div (och bandbredd) kommer samplingshastigheten att minska.
Så frågan är vilken kvalitet en FFT-mätning har som är gjord på 600 MHz sinusvåg? Ser vi tillbaka på FFT-mätningen i fig 1 kan vi lägga märke till den enda frekvensspik, med tillhörande markör som visar 0 dBm effekt vid runt 600 MHz. Det svara mot förväntningarna, men FFT-svaret ser mycket "brett" ut för att vara en signal med en enda frekvens.
Avståndet mellan linjerna i frekvensspektrum från FFT-omvandlingen, eller bredden på frekvens-”bucklorna” som pekar ut signalenergin kallas "upplösningsbandbredd" (resolution bandwidth). Det är strängt baserat på tidslängden av inhämtade data och den faktor som valts för FFT-fönstret. Ett rektangulärt fönster används här, med en faktor av "1", vilket innebär att upplösningsbandbredd helt enkelt är det inverterade värdet av tidsignalen. Så gäller i detta exempel:
ResBW = 1 / (1 nsec / ruta × 10 rutor) = 100 MHz
Så denna FFT kunde utskilja frekvenskomponenter i signalspektrum så nära som 100 MHz, men alla komponenter som ligger närmare än 100 MHz läggs ihop och kan omöjligen skiljas ut. Detta är faktiskt en riktigt grov mätning.

Ökad tid på skärmen förbättrar FFT-svaret
För demonstrera hur inspelad tid påverkar FFT-resultatet, om tiden/ruta panoreras till 200 ns/ruta, med en ny inspelad tid av 2 µs över skärmen, ändras upplösningsbandbredden drastiskt till:
ResBW = 1 / (200 ns / div × 10 divisioner) = 500 kHz
Den stora förändringen i FFT-resultatet kan ses i fig 2. 600 MHz-spiken har mycket finare upplösning. Vi ser här en avvägning: Nu bearbetas flera tidssamples, FFT-beräkningen ger fler spektrallinjer och bättre upplösningsbandbredd. Men mätningen körs långsammare än tidigare för att behandla mer data.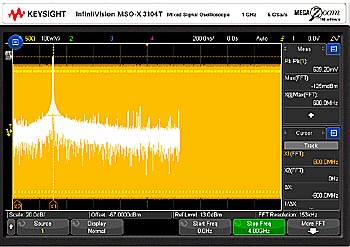

Fig 2. Inhämtningen i tidsdomänen görs här vid 200 nsec/ div och vi ser resultet av FFT-beräkningen med en inmatad 600 MHz sinusvåg.

Start-, stopp- och mittfrekvens och spann
En viktig förmåga i FFT-beräkning och dess resultat vi ser är möjligheten att kunna zooma in i ett område av intresse för analys. I vårt första exempel hade vi ett brett spann från 0 Hz till 2,5 GHz så det var svårt att se några detaljer runt 600 MHz-bärvågen. Antag att det fanns en misstanke om störning runt 600 MHz bärvåg och att vi önskade kunna inspektera den. VI kan ställa in FFT runt en centerfrekvens på 600 MHz och önskat spann, såsom 100 MHz runt 600 MHz-bärvågen. En Startfrekvens 550 MHz och stoppfrekvens på 650 MHz kunde också ha valts med samma resultat. En sådan en FFT mätning, med dessa parametrar, kan ses i fig 3.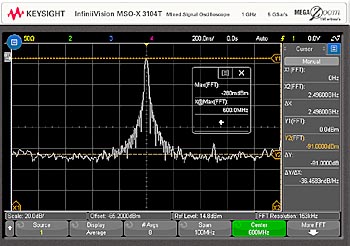

Fig 3. FFT av en 600 MHz sinusvåg FFT ställts in för 600 MHz mittfrekvens och 100 MHz spann.

Bredbandig FFT-analys
Allt fler av dagens signaler är modulerade vilket kan öka den spektralbredden till 100-tals MHz eller till och med flera GHz. Om den spektrala bandbredden är högre än omkring 500 MHz har dagens spektrumanalysatorer eller vektor-signalanalysatorer inte har tillräckligt med analysbandbredd för att åstadkomma meningsfulla mätningar. I sådana fall krävs ett oscilloskop eller digitaliserare med tillräckligt analysbandbredd för uppgiften. Frekvensen hos bärvågen av intresse är också viktigt. Testsignalens bärfrekvens plus halva spektralbredden av denna signal måste vara mindre än eller lika med oscilloskopet bandbredd för att oscilloskopet som skall användas på egen hand för mätningen. Mätningen måste ta hänsyn till mätning av en bredbandig signal i frekvensplanet.
Signalen som testas är en 600 MHz är ett RF-pulståg, med 4 µs breda RF-pulser som upprepas var 20:e µs. Det är en linjär frekvensmodulering av signalen som sveper bärfrekvensen från 300 MHz vid början av RF-pulsens envelop till 900 MHz vid slutet av pulssvepet.
För att i grunden genomföra en FFT-mätning av RF-pulsen är ett första steg att fånga in en puls av signalen på skärmen i tidsdomänen. Oscilloskopet återställs till ett känt tillstånd genom att trycka på "Default Setup." "Auto Scale" trycks in och inställningen tid/ruta justeras för att få en huvudpuls på skärmen. Utgångsläget,  trigg på stigande flank, stärks ytterligare med ”trigger holdoff”. Detta säkerställer att en trigger inte händer mitt i en puls eftersom det skulle skapa instabilitet i den infångat svep. ”Trigg holdoff” är satt till en tid som är något lite längre än bredden av RF-pulsen. RF-pulsen är 4 µs bred, så en ”trigger holdoff” av 5 µs fungerar bra.
Därefter trycks "FFT" -knappen in för att räkna fram en spektral bild av RF-pulståget från tidsdomänen av den digitaliserade signalen på skärmen. Det finns FFT-kontroller för start- och stoppfrekvens eller cancerfrekvens och spann.
Ett brett spann väljs först, med en startfrekvens av 0 Hz och en stoppfrekvens på 2,5 GHz. Eftersom detta är en pulssignal, och en hel puls kan placeras på skärmen med enbart brus på vänster och höger sida av oscilloskopskärmen har ett rektangulärt fönster valts för att beräkna FFT. FFT-medelvärdesbildning, med 8 genomföranden, hjälper också till att optimera mätresultatet. Det resulterande FFT-svaret visas i fig 4.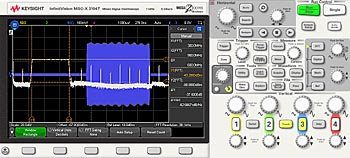

Fig 4. FFT av 4 µs breda pulser med 20 µs upprepning i ett linjärt FM-svep.

Markörer placerades på FFT-svaret och vi kan se att denna RF-puls har ett 600 MHz brett spektrum, från 300 MHz till 900 MHz. Vad vi ännu inte har bevisat är att frekvensen av bärvågen skiftar från 300 MHz till 900 MHz, linjärt, från vänster sida av pulsen, över till den högra sidan av pulsen.

Grindad FFT-beräkning
Ett sätt att snabbt se några bärarvågors frekvensvärden över pulsen är att använda den grindade FFT-funktionen. Detta aktiveras genom att slå på tidsgrindning av svep i den normala tidsdomänen. Det finns en knapp med ett förstoringsglas som trycks in för att aktivera det här läget. När denna knapp tryckts in visas det normala tidssvepet på den övre halvan av skärmen, och sedan en förstorad bild längst ner på skärmen. Med tid/ruta-kontrollen expanderar och krymper det tidsgrindade fönstret  som är placerat på det övre, normal spåret och med kontrollen för tidsfördröjning flyttas fönstret längs spåret. Oavsett vilken del av vågformen i detta fönster dyker den upp i det nedre spåret, men förstorad.
Ett intressant mätresultat från att skapa en liten tidsbredd fönsterfunktion och sedan flytta den till början av pulsen. FFT beräknas från de data som finns inom det grindade tidsfönstret. Detta visas i figuren nedan.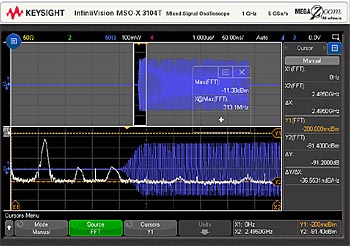

Fig 5. Med tidsgrindad FFT-funktion kan bärvågen i början av RF-pulsen observeras.

FFT-mätning av toppamplituden och frekvensen hos spiken visar att RF-pulsen börjar med en bärfrekvens runt 300 MHz. Om tidsgrindfönstret flyttas till mitten av RF-pulsen verkar frekvensen ligga runt 600 MHz. Och slutet av RF-pulsen är frekvensen 900 MHz. Detta verkar vara ett linjär frekvensmodulerad svep, såsom önskas.

Frekvensmätning och matematiska funktioner
I vissa fall kan en matematisk funktion för mätningar kan ge ett användbar vy av profilen för ett frekvenssvep. Oscilloskopet kan visa upp till 1000 mätningar i ett mätinstrumentinriktat ("measurement trend") format. På ett liknande signalexempel behöver man verifiera ett 600 ns brett pulståg som upprepas var 20 µs. FFT-funktionen är nu avstängd och tidsmätningar i renodlad tidsdomän görs.
Först ändras oscilloskopets insamlingsmetod från "normal" till "högupplöst". För det andra väljer man frekvensmätning från listan över möjliga mätningar genom att trycka på "measure"-knappen. En medelhög tröskel för detektering av bärvågens nollgenomgång är satt till 30 mV eftersom bärvågens sving limmer mellan ca -316 mV och 316 mV (1 mW signal, 0 dBm över 50 ohm). Därefter trycker man in ”Math"-tangenten trycks och väljer den mattefunktion som kallas "Measurement trend" väljs. Markörer delas ha sin källa vara matten funktionen resultatet. En intressant bild av frekvensmätningar tagna tvärs RF-pulsen kan ses i fig 6.
{mosimage}
Fig 6. Mätning av trend hos pulsen med mattefunktionen "Frequency".

Tydligt är att pulsens bärvåg ändras på ett linjärt sätt över över pulsen, från vänster till höger, som avsett. Lägg märke till att den linjära rampen som visas inte går tvärs över RF-pulsens hela bredd. Det beror på att gränsen för 1000 beräkningar har nåtts. Det viktiga är att en del av den pulsade FM-funktionen kan ses och den är linjär. För att frekvensmätningar över pulsen skall ha tillräckligt precision var det viktigt att "högupplöst" insamlingsläge valdes.

FFT viktigt verktyg
FFT i oscilloskop är ett värdefullt verktyg för att kunna se en signal i frekvensdomänen. Detta kan ytterst genomföras med mycket stor bandbredd för att möjliggöra mätningar som inte kan genomföras med vektorsignalmätare. Som exempel kunde FFT-mätningar verifiera att en linjärt svept  FM-signal ändrade bärfrekvens på det sätt som det skulle.
Det fanns också en plats för andra matematiska funktioner, nämligen mätning av trender. I detta exempel gjordes en sådan beräkning för en mycket enkel verifiering av ett linjärt FM-svep.

Om författaren
Brad Frieden är marknadsföringsingenjör och produktplanerare inom divisionen för oscilloskop och protokoll inom Keysight. Han har varit inriktad på generellt användbara logikanalysatorer och deras tillämpningar samt flyg/försvarsrelaterade RF-mätningar där man använt oscilloskop med hög bandbredd och minnen med stort minnesdjup. Han har arbetat hos HP/Agilent under 30 år och varit inblandad i en mängd olika marknadsföringsroller inom områden som test inom fiberoptik, pulsgeneratorer, oscilloskop, och logikanalysatorer. Han tog sin BSEE vid Texas Tech 1981 och MSEE vid The University of Texas 1991.

Filed under: Matteknik